how to find proportion in statistics with mean and standard deviation

6.3 The Sample Proportion

Learning Objectives

1. To recognize that the sample proportion $\widehat{P}$ is a random variable.
2. To sympathise the pregnant of the formulas for the mean and standard difference of the sample proportion.
3. To acquire what the sampling distribution of $\widehat{P}$ is when the sample size is large.

Often sampling is done in order to estimate the proportion of a population that has a specific characteristic, such as the proportion of all items coming off an assembly line that are defective or the proportion of all people inbound a retail store who brand a purchase before leaving. The population proportion is denoted p and the sample proportion is denoted $\widehat{p}.$ Thus if in reality 43% of people entering a store make a purchase earlier leaving, p = 0.43; if in a sample of 200 people entering the store, 78 make a purchase, $\widehat{p}=78/200=0.39.$

The sample proportion is a random variable: it varies from sample to sample in a mode that cannot be predicted with certainty. Viewed every bit a random variable it volition exist written $\widehat{P}.$ It has a meanThe number near which proportions computed from samples of the aforementioned size center. ${\mathit{\mu }}_{\widehat{P}}$ and a standard deviationA measure of the variability of proportions computed from samples of the aforementioned size. ${\mathit{\sigma }}_{\widehat{P}}.$ Here are formulas for their values.

Suppose random samples of size northward are drawn from a population in which the proportion with a characteristic of interest is p. The hateful ${\mathit{\mu }}_{\widehat{P}}$ and standard deviation ${\mathit{\sigma }}_{\widehat{P}}$ of the sample proportion $\widehat{P}$ satisfy

$${\mathit{\mu }}_{\widehat{P}}=p\text{and}{\mathit{\sigma }}_{\widehat{P}}=\sqrt{\frac{pq}{\mathrm{north}}}$$

where $q=1-p.$

The Key Limit Theorem has an analogue for the population proportion $\widehat{P}.$ To run across how, imagine that every element of the population that has the characteristic of interest is labeled with a 1, and that every element that does not is labeled with a 0. This gives a numerical population consisting entirely of zeros and ones. Clearly the proportion of the population with the special feature is the proportion of the numerical population that are ones; in symbols,

$$p=\frac{\text{number}\text{of}\mathrm{one}\text{s}}{\mathrm{Due\; north}}$$

But of course the sum of all the zeros and ones is merely the number of ones, so the mean μ of the numerical population is

$$\mathit{\mu }=\frac{{\displaystyle \mathrm{\Sigma }\mathrm{10}}}{\mathrm{North}}=\frac{\text{number}\text{of}1\text{s}}{N}$$

Thus the population proportion p is the same equally the mean μ of the corresponding population of zeros and ones. In the same way the sample proportion $\widehat{p}$ is the same every bit the sample hateful $\stackrel{-}{\mathit{x}}.$ Thus the Key Limit Theorem applies to $\widehat{P}.$ Nonetheless, the condition that the sample be large is a little more complicated than just being of size at least 30.

The Sampling Distribution of the Sample Proportion

For large samples, the sample proportion is approximately usually distributed, with mean ${\mathit{\mu }}_{\widehat{P}}=p$ and standard deviation ${\mathit{\sigma }}_{\widehat{P}}=\sqrt{pq/\mathrm{north}}.$

A sample is large if the interval $\left[p\text{−}\mathrm{three}{\mathit{\sigma }}_{\widehat{P}},p+3{\mathit{\sigma }}_{\widehat{P}}\right]$ lies wholly inside the interval $\left[\mathrm{0,i}\right].$

In actual practice p is not known, hence neither is ${\mathit{\sigma }}_{\widehat{P}}.$ In that case in order to check that the sample is sufficiently big nosotros substitute the known quantity $\widehat{p}$ for p. This means checking that the interval

$$\left[\widehat{p}\text{−}\mathrm{three}\sqrt{\frac{\widehat{p}(1-\widehat{p})}{\mathrm{due\; north}}},\widehat{p}+\mathrm{iii}\sqrt{\frac{\widehat{p}(1-\widehat{p})}{\mathrm{northward}}}\right]$$

lies wholly within the interval $\left[\mathrm{0,1}\right].$ This is illustrated in the examples.

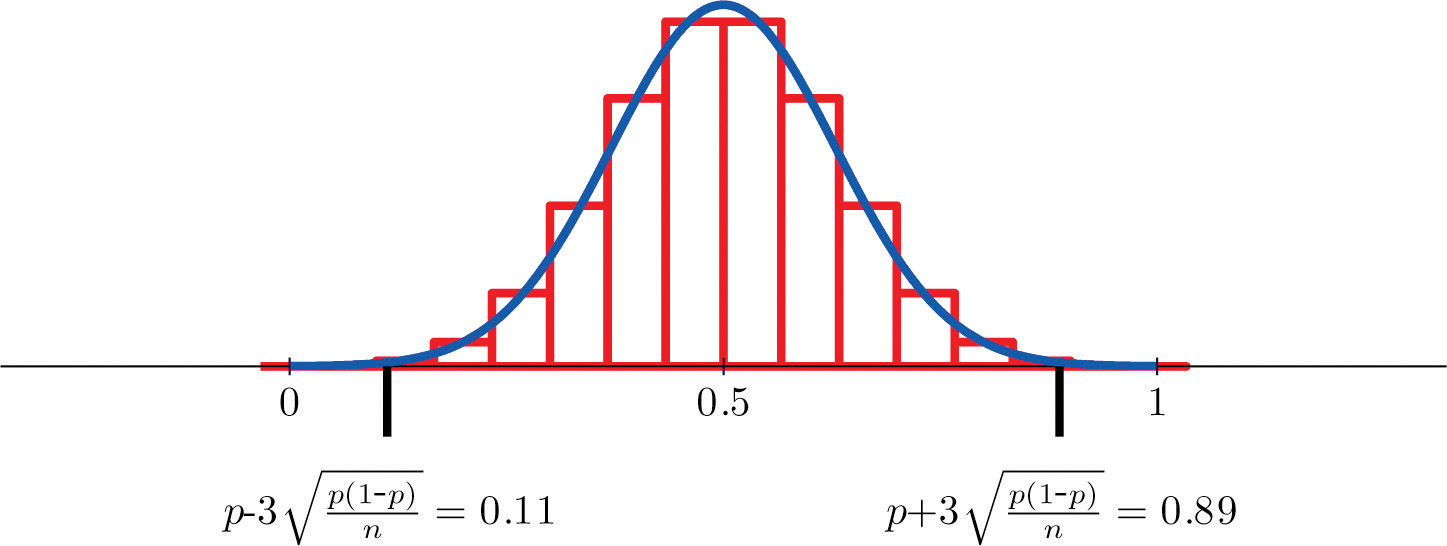
Figure 6.5 "Distribution of Sample Proportions" shows that when p = 0.1 a sample of size 15 is too pocket-size merely a sample of size 100 is acceptable. Figure 6.6 "Distribution of Sample Proportions for " shows that when p = 0.5 a sample of size 15 is acceptable.

Figure 6.5 Distribution of Sample Proportions

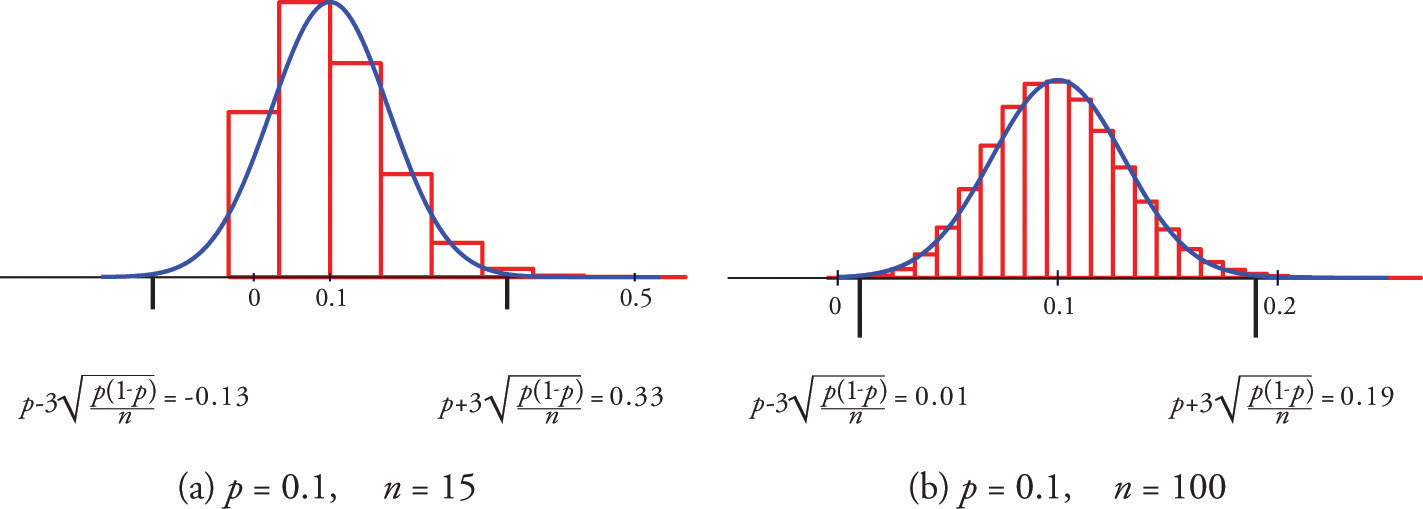
Figure 6.half dozen Distribution of Sample Proportions for p = 0.5 and n = 15

Example vii

Suppose that in a population of voters in a certain region 38% are in favor of particular bond effect. Nine hundred randomly selected voters are asked if they favor the bond issue.

1. Verify that the sample proportion $\widehat{P}$ computed from samples of size 900 meets the condition that its sampling distribution be approximately normal.
2. Detect the probability that the sample proportion computed from a sample of size 900 volition be within 5 percentage points of the true population proportion.

Solution

1. The information given is that p = 0.38, hence $q=\mathrm{ane}-p=0.62.$ First nosotros use the formulas to compute the hateful and standard departure of $\widehat{P}$ :

   $${\mathit{\mu }}_{\widehat{P}}=p=0.38\text{and}{\mathit{\sigma }}_{\widehat{P}}=\sqrt{\frac{pq}{n}}=\sqrt{\frac{\left(0.38\right)\left(0.62\right)}{900}}=0.01618$$

   And then $3{\mathit{\sigma }}_{\widehat{P}}=3\left(0.01618\right)=0.04854\approx 0.05$ so

   $$\left[p\text{−}3{\mathit{\sigma }}_{\widehat{P}},p+\mathrm{three}{\mathit{\sigma }}_{\widehat{P}}\right]=\left[0.38-0.\mathrm{05,0}.38+0.05\right]=\left[0.\mathrm{33,0}.43\right]$$

   which lies wholly within the interval $\left[\mathrm{0,1}\right]$ , and then information technology is safe to assume that $\widehat{P}$ is approximately commonly distributed.

2. To be within 5 percentage points of the true population proportion 0.38 means to be between $0.38-0.05=0.33$ and $0.38+0.05=0.43.$ Thus

   $$\begin{array}{ll}P(0.33<\widehat{P}<0.43)\hfill & =P\left(\frac{0.33-{\mathit{\mu }}_{\widehat{P}}}{{\mathit{\sigma }}_{\widehat{P}}}<Z<\frac{0.43-{\mathit{\mu }}_{\widehat{P}}}{{\mathit{\sigma }}_{\widehat{P}}}\right)\hfill \\ \hfill & =P\left(\frac{0.33-0.38}{0.01618}<Z<\frac{0.43-0.38}{0.01618}\right)\hfill \\ \hfill & =P\left(\text{−}3.09<Z<3.09\right)\hfill \\ \hfill & =P\left(3.09\right)-P\left(\text{−}\mathrm{iii.09}\right)\hfill \\ \hfill & =0.9990-0.0010=0.9980\hfill \end{array}$$

Example 8

An online retailer claims that 90% of all orders are shipped within 12 hours of being received. A consumer group placed 121 orders of different sizes and at different times of day; 102 orders were shipped within 12 hours.

1. Compute the sample proportion of items shipped within 12 hours.
2. Confirm that the sample is big enough to assume that the sample proportion is unremarkably distributed. Use p = 0.ninety, respective to the supposition that the retailer'southward claim is valid.
3. Assuming the retailer's merits is truthful, observe the probability that a sample of size 121 would produce a sample proportion and then low every bit was observed in this sample.
4. Based on the answer to part (c), depict a determination almost the retailer's claim.

Solution

1. The sample proportion is the number x of orders that are shipped within 12 hours divided by the number n of orders in the sample:

   $$\widehat{p}=\frac{x}{\mathrm{north}}=\frac{102}{121}=0.84$$

2. Since p = 0.xc, $q=1-p=0.10$ , and north = 121,

   $${\mathit{\sigma }}_{\widehat{P}}=\sqrt{\frac{\left(0.90\right)\left(0.10\right)}{121}}=0.0\stackrel{-}{27}$$

   hence

   $$\left[p\text{−}3{\mathit{\sigma }}_{\widehat{P}},p+3{\mathit{\sigma }}_{\widehat{P}}\right]=\left[\mathrm{0.ninety}-0.\mathrm{08,0}.90+0.08\right]=\left[0.\mathrm{82,0}.98\right]$$

   Considering $$\left[0.82,0.98\right]\subset \left[\mathrm{0,1}\right],$$ information technology is appropriate to use the normal distribution to compute probabilities related to the sample proportion $\widehat{P}.$

3. Using the value of $\widehat{P}$ from office (a) and the computation in part (b),

   $$\begin{array}{ll}P(\widehat{P}\le 0.84)\hfill & =P\left(Z\le \frac{0.84-{\mathit{\mu }}_{\widehat{P}}}{{\mathit{\sigma }}_{\widehat{P}}}\right)\hfill \\ \hfill & =P\left(Z\le \frac{0.84-\mathrm{0.xc}}{0.0\stackrel{-}{27}}\right)\hfill \\ \hfill & =P\left(Z\le \text{−}\mathrm{two.20}\right)=0.0139\hfill \end{array}$$
4. The computation shows that a random sample of size 121 has only virtually a 1.iv% chance of producing a sample proportion as the 1 that was observed, $\widehat{p}=0.84$ , when taken from a population in which the actual proportion is 0.90. This is so unlikely that it is reasonable to conclude that the actual value of p is less than the 90% claimed.

Key Takeaways

• The sample proportion is a random variable $\widehat{P}.$
• At that place are formulas for the hateful ${\mathit{\mu }}_{\widehat{P}}$ and standard deviation ${\mathit{\sigma }}_{\widehat{P}}$ of the sample proportion.
• When the sample size is large the sample proportion is normally distributed.

Exercises

Bones

1. The proportion of a population with a characteristic of involvement is p = 0.37. Find the hateful and standard departure of the sample proportion $\widehat{P}$ obtained from random samples of size one,600.

2. The proportion of a population with a characteristic of interest is p = 0.82. Find the hateful and standard difference of the sample proportion $\widehat{P}$ obtained from random samples of size 900.

3. The proportion of a population with a characteristic of interest is p = 0.76. Find the mean and standard deviation of the sample proportion $\widehat{P}$ obtained from random samples of size one,200.

4. The proportion of a population with a characteristic of interest is p = 0.37. Discover the hateful and standard deviation of the sample proportion $\widehat{P}$ obtained from random samples of size 125.

5. Random samples of size 225 are drawn from a population in which the proportion with the characteristic of interest is 0.25. Decide whether or not the sample size is large enough to presume that the sample proportion $\widehat{P}$ is normally distributed.

6. Random samples of size 1,600 are drawn from a population in which the proportion with the characteristic of interest is 0.05. Determine whether or non the sample size is big plenty to presume that the sample proportion $\widehat{P}$ is normally distributed.

7. Random samples of size n produced sample proportions $\widehat{p}$ as shown. In each case make up one's mind whether or not the sample size is big enough to presume that the sample proportion $\widehat{P}$ is normally distributed.

   1. northward = 50, $\widehat{p}=0.48$
   2. n = l, $\widehat{p}=0.12$
   3. n = 100, $\widehat{p}=0.12$

8. Samples of size n produced sample proportions $\widehat{p}$ as shown. In each case decide whether or not the sample size is large enough to assume that the sample proportion $\widehat{P}$ is unremarkably distributed.

   1. northward = 30, $\widehat{p}=0.72$
   2. northward = xxx, $\widehat{p}=0.84$
   3. n = 75, $\widehat{p}=0.84$

9. A random sample of size 121 is taken from a population in which the proportion with the characteristic of interest is p = 0.47. Find the indicated probabilities.

   1. $P\left(0.45\le \widehat{P}\le 0.50\right)$
   2. $P\left(\widehat{P}\ge 0.50\right)$

10. A random sample of size 225 is taken from a population in which the proportion with the characteristic of interest is p = 0.34. Find the indicated probabilities.

    1. $P\left(0.25\le \widehat{P}\le 0.40\right)$
    2. $P\left(\widehat{P}\le 0.35\right)$

11. A random sample of size 900 is taken from a population in which the proportion with the characteristic of interest is p = 0.62. Notice the indicated probabilities.

    1. $P\left(0.60\le \widehat{P}\le 0.64\right)$
    2. $P\left(0.57\le \widehat{P}\le 0.67\right)$

12. A random sample of size one,100 is taken from a population in which the proportion with the feature of interest is p = 0.28. Observe the indicated probabilities.

    1. $P\left(0.27\le \widehat{P}\le 0.29\right)$
    2. $P\left(0.23\le \widehat{P}\le 0.33\right)$

Applications

13. Suppose that 8% of all males endure some form of color blindness. Find the probability that in a random sample of 250 men at least 10% will endure some form of color blindness. First verify that the sample is sufficiently big to use the normal distribution.

14. Suppose that 29% of all residents of a customs favor annexation by a nearby municipality. Detect the probability that in a random sample of 50 residents at least 35% will favor annexation. First verify that the sample is sufficiently large to utilise the normal distribution.

15. Suppose that 2% of all jail cell telephone connections by a certain provider are dropped. Find the probability that in a random sample of i,500 calls at most 40 volition be dropped. First verify that the sample is sufficiently large to utilise the normal distribution.

16. Suppose that in 20% of all traffic accidents involving an injury, driver distraction in some form (for case, changing a radio station or texting) is a factor. Notice the probability that in a random sample of 275 such accidents between 15% and 25% involve driver lark in some form. First verify that the sample is sufficiently large to use the normal distribution.

17. An airline claims that 72% of all its flights to a certain region arrive on fourth dimension. In a random sample of 30 recent arrivals, 19 were on fourth dimension. You may presume that the normal distribution applies.

    1. Compute the sample proportion.
    2. Assuming the airline's claim is true, notice the probability of a sample of size xxx producing a sample proportion then depression as was observed in this sample.

18. A humane society reports that 19% of all pet dogs were adopted from an animate being shelter. Assuming the truth of this assertion, notice the probability that in a random sample of 80 pet dogs, betwixt 15% and 20% were adopted from a shelter. You may presume that the normal distribution applies.

19. In one report it was plant that 86% of all homes have a functional fume detector. Suppose this proportion is valid for all homes. Discover the probability that in a random sample of 600 homes, between 80% and 90% will accept a functional smoke detector. You may assume that the normal distribution applies.

20. A state insurance commission estimates that xiii% of all motorists in its state are uninsured. Suppose this proportion is valid. Find the probability that in a random sample of 50 motorists, at least five volition be uninsured. You may assume that the normal distribution applies.

21. An outside financial auditor has observed that about 4% of all documents he examines contain an error of some sort. Assuming this proportion to exist accurate, find the probability that a random sample of 700 documents volition contain at least xxx with some sort of error. You lot may assume that the normal distribution applies.

22. Suppose seven% of all households take no home telephone merely depend completely on cell phones. Find the probability that in a random sample of 450 households, between 25 and 35 will have no habitation phone. Yous may presume that the normal distribution applies.

Additional Exercises

23. Some countries allow individual packages of prepackaged goods to counterbalance less than what is stated on the package, bailiwick to sure weather, such equally the boilerplate of all packages being the stated weight or greater. Suppose that one requirement is that at near iv% of all packages marked 500 grams tin weigh less than 490 grams. Assuming that a product actually meets this requirement, observe the probability that in a random sample of 150 such packages the proportion weighing less than 490 grams is at least 3%. You may assume that the normal distribution applies.

24. An economist wishes to investigate whether people are keeping cars longer now than in the by. He knows that five years ago, 38% of all rider vehicles in performance were at to the lowest degree ten years old. He commissions a report in which 325 automobiles are randomly sampled. Of them, 132 are ten years old or older.

    1. Find the sample proportion.
    2. Observe the probability that, when a sample of size 325 is drawn from a population in which the truthful proportion is 0.38, the sample proportion will be as large as the value you computed in part (a). Y'all may presume that the normal distribution applies.
    3. Give an interpretation of the result in role (b). Is there strong prove that people are keeping their cars longer than was the case 5 years ago?

25. A country public health department wishes to investigate the effectiveness of a entrada against smoking. Historically 22% of all adults in the country regularly smoked cigars or cigarettes. In a survey commissioned by the public health department, 279 of 1,500 randomly selected adults stated that they smoke regularly.

    1. Discover the sample proportion.
    2. Find the probability that, when a sample of size ane,500 is drawn from a population in which the true proportion is 0.22, the sample proportion will be no larger than the value you computed in part (a). Y'all may assume that the normal distribution applies.
    3. Give an interpretation of the outcome in function (b). How strong is the show that the campaign to reduce smoking has been constructive?

26. In an try to reduce the population of unwanted cats and dogs, a group of veterinarians prepare upwards a low-cost spay/neuter dispensary. At the inception of the clinic a survey of pet owners indicated that 78% of all pet dogs and cats in the customs were spayed or neutered. After the low-toll clinic had been in operation for three years, that figure had risen to 86%.

    1. What information is missing that you would need to compute the probability that a sample drawn from a population in which the proportion is 78% (corresponding to the supposition that the low-toll clinic had had no effect) is equally loftier as 86%?
    2. Knowing that the size of the original sample three years ago was 150 and that the size of the contempo sample was 125, compute the probability mentioned in part (a). You may presume that the normal distribution applies.
    3. Give an interpretation of the result in part (b). How stiff is the testify that the presence of the low-price clinic has increased the proportion of pet dogs and cats that accept been spayed or neutered?

27. An ordinary die is "off-white" or "balanced" if each face has an equal take a chance of landing on tiptop when the dice is rolled. Thus the proportion of times a three is observed in a big number of tosses is expected to be close to ane/vi or $\mathrm{0.ane}\stackrel{-}{6}.$ Suppose a die is rolled 240 times and shows iii on top 36 times, for a sample proportion of 0.15.

    1. Find the probability that a off-white dice would produce a proportion of 0.15 or less. You may assume that the normal distribution applies.
    2. Give an interpretation of the event in part (b). How strong is the evidence that the die is not fair?
    3. Suppose the sample proportion 0.15 came from rolling the die 2,400 times instead of only 240 times. Rework office (a) under these circumstances.
    4. Requite an interpretation of the consequence in role (c). How strong is the evidence that the dice is not off-white?

Answers

1. ${\mathit{\mu }}_{\widehat{P}}=0.37$ , ${\mathit{\sigma }}_{\widehat{P}}=0.012$

3. ${\mathit{\mu }}_{\widehat{P}}=0.76$ , ${\mathit{\sigma }}_{\widehat{P}}=0.012$

5. $p\pm 3\sqrt{\frac{pq}{n}}=0.25\pm 0.087$ , yes

7. 1. $\widehat{p}\pm \mathrm{iii}\sqrt{\frac{\widehat{p}\widehat{q}}{n}}=0.48\pm 0.21$ , yep
   2. $\widehat{p}\pm 3\sqrt{\frac{\widehat{p}\widehat{q}}{\mathrm{northward}}}=0.12\pm \mathrm{0.fourteen}$ , no
   3. $\widehat{p}\pm \mathrm{iii}\sqrt{\frac{\widehat{p}\widehat{q}}{n}}=0.12\pm 0.10$ , yep
9. 1. 0.4154
   2. 0.2546
11. 1. 0.7850
    2. 0.9980

13. $p\pm \mathrm{three}\sqrt{\frac{pq}{\mathrm{northward}}}=0.08\pm 0.05$

    and

    $\left[0.\mathrm{03,0}.13\right]\subset \left[\mathrm{0,1}\right],0.1210$

15. $p\pm \mathrm{three}\sqrt{\frac{pq}{\mathrm{northward}}}=0.02\pm 0.01$

    and

    $\left[0.\mathrm{01,0}.03\right]\subset \left[\mathrm{0,1}\right],0.9671$

17. 1. 0.63
    2. 0.1446

19. 0.9977

21. 0.3483

23. 0.7357

25. 1. 0.186
    2. 0.0007
    3. In a population in which the true proportion is 22% the gamble that a random sample of size 1500 would produce a sample proportion of 18.vi% or less is just seven/100 of 1%. This is strong testify that currently a smaller proportion than 22% fume.
27. 1. 0.2451
    2. Nosotros would expect a sample proportion of 0.15 or less in near 24.5% of all samples of size 240, so this is practically no bear witness at all that the die is not fair.
    3. 0.0139
    4. We would expect a sample proportion of 0.xv or less in merely almost 1.4% of all samples of size 2400, and then this is strong evidence that the die is not fair.

Source: https://saylordotorg.github.io/text_introductory-statistics/s10-03-the-sample-proportion.html

Posted by: andrewswitis1960.blogspot.com

Share this post